In this first part of a two-part series, we develop a direct approach to measuring credit risk at the transaction level. Under this approach, we identify credit risk as a "cost" — most simply, the cost of buying credit "insurance" which transfers the risk to the seller (see [1] and [2]). The emerging credit derivatives market promises to provide a much stronger, empirical foundation for estimating credit risk costs. Financial institutions have a high stake in this quest for better measures of credit risk. Such measures are fundamental to their efforts to account properly for credit risk in both pricing and portfolio management.

The approach here emphasizes that every credit instrument has an associated risk premium. This premium corresponds to the competitively determined cost of a form of credit insurance. In what follows, we develop the basic risk premium concept, and provide some simple numerical examples. In part two of this series, we investigate the relationship between risk premiums and portfolio value at risk.

Understanding Credit Risk Premiums

In describing credit risk, analysts have attached different meanings to the term risk premium. In some contexts, the term denotes a payment compensating for both (1) the expected or actuarial value of losses associated with an instrument and (2) the (downside) volatility that the instrument contributes to a diversified investment portfolio. In other contexts, analysts view only the second of these components as representing risk. They then use the term risk premium more narrowly in referring only to the uncertain component of credit loss. For clarity, we will label the first component as the expected loss (EL) risk premium and the second as the unexpected loss (UL) risk premium (see [3]).

In discussing casualty and other forms of commercial insurance, a "premium" represents the cost paid by the policyholder to transfer loss risk to the issuer of the policy. Most often, the premium covers both expected and unexpected loss as described above. However, in reinsurance and other structures, the coverage corresponds mainly to a portion of unexpected loss.

This insurance perspective helps in understanding credit derivatives. The counter-party acquiring risk in the credit derivative transaction essentially sells credit insurance. The cost of this insurance constitutes the "risk premium." In the case of a credit default swap, the party ceding risk purchases essentially a constant premium term insurance policy covering credit loss on a specific loan. As an alternative, the financial institution could purchase a "put option" on the credit loss, in which case it would make a single up-front payment for the protection. We then view the up-front payment as an option premium.

If a commercial financial institution chooses to hold an exposure and thus "self-insure" against credit loss, some portion of loan revenue must implicitly go to support the risk capital the financial institution holds to cover its unexpected credit losses. Normal reserving covers expected credit loss. In this context, one can think of the commercial lending line of business within a bank as internally transferring some portion of its loan revenue into a risk capital account. Distributions from this account provide bank shareholders with a return on their risk capital. Since the credit risk is borne mostly by the shareholders, the return on their risk capital amounts to a risk (insurance) premium paid by the commercial lending line of business.

We will define the risk premium associated with a credit instrument in a way that focuses on the cost of swapping unexpected total return, i.e., deviations from expected total return, as opposed to the cost of insuring against unexpected default loss. Before writing down the specific concept, we need to lay some groundwork. Specifically, we need to distinguish between the "natural" probability measure governing credit rating migration and the associated "risk-neutral" migration measure.

Natural Measure and Risk-Neutral Measure for Risk Rating Migration

We assume that the borrower can be assigned a discrete credit rating grade that represents a sufficient statistic for predicting credit losses. This rating grade could come from a public rating agency or, alternatively, the lender’s internal risk rating system. We refer to the probability measure that governs the risk rating migration of the borrower over time as the natural process measure.

The theory of risk-neutral valuation specifies that, under certain conditions, contingent claims can be priced uniquely by arbitrage (see [4]). In particular, and most importantly, the underlying instrument(s) governing the contingent claim must trade in a market free of arbitrage opportunities. In the present context, that market is the secondary commercial loan market. In the past, loans have generally been regarded as "buy and hold" assets for originators. In recent years, however, trading volumes and liquidity in the large corporate market have improved substantially, making the arbitrage-free assumption more plausible. It would take us far afield to discuss the justification and detailed methods for applying arbitrage pricing theory to commercial loans and credit derivatives. We instead refer the interested reader to [3] and [5].

In any case, our point of departure is that arbitrage pricing theory applies to credit markets and provides an internally consistent and empirically supported framework for pricing. Under this hypothesis, one may calculate the arbitrage-driven market price of a commercial loan or credit derivative as the expected net present value of the cash flows it generates. This expectation calculation, however, needs a particular probability measure. We use not the natural process measure, but rather a related measure, technically referred to as the (unique) equivalent martingale process measure, but more commonly known as the risk-neutral process measure. We again refer the reader to [3] and [5] for a detailed discussion of the formal procedure for constructing the risk-neutral migration measure associated with a given natural migration measure.

In what follows, we use the notation  to denote the expectation of the random variable  with respect to the natural migration measure, and  to denote expectation of  with respect to risk-neutral measure.

Defining Credit Risk Premiums

We take as the definition of unexpected total return (UTR) risk premium:

,            (1)

where V denotes the net present value (NPV) to the lender of the credit instrument cash flows. The possibility of credit loss makes V a random variable. In general, the discounting used in calculating V involves the risk-free short rate of interest r. If one models interest rates as having a stochastic term structure, then the expectation operators in (1) will reflect the joint interest rate and credit migration process. In the present context, we will restrict attention to the simple case in which the short rate is known deterministically.

The UTR risk premium as defined in (1) is the difference between the NPV the lender expects to realize by holding the credit instrument for its cash flows and the price he would obtain by selling the instrument at its (arbitrage determined) fair market value. The UTR risk premium therefore represents the economic incentive to the lender to bear the risk associated with holding the instrument.

To gain some insight into this particular definition of risk premium, we consider a commercial lender who manages his activity using two separate accounts: an operating account, which processes cash flows, and a capital account, where profits and losses normally occur. The capital account receives a risk premium paid out of the operating account. In exchange, the capital account makes payments into the operating account to offset any "unexpected" loan revenue,  (see Table 1).
 
 

	Front-End UTR Risk Premium	Loan Revenue	Back-End Settlement	Net Cash Flow
Operating Account
Capital Account

The net cash flow into the operating account has present value , independently of the actual loan revenue V. The effect is therefore equivalent to the sale of the loan at its fair (arbitrage determined) market value. The net cash flow into (or out of) the capital account is , so the capital account has effectively purchased the loan at its market value.

One way of viewing the transaction is that by paying the risk premium the operating account enters into a form of credit swap with the capital account, exchanging a risky set of cash flows with return V for a riskless set of cash flows with return . Two cash exchanges occur: (i) the front-end payment by the operating account to the capital account of the risk premium and (ii) the back-end settlement between the two accounts to offset the unexpected loss/gain in the operating account. Note that the expected value of the back-end settlement is zero.

It is important to distinguish between the unexpected total return (UTR) risk premium, which is really the cost of a credit swap, and the unexpected default loss (UDL) risk premium, which is the "premium" on a default loss insurance "policy." In the case of the swap, the financial institution is transferring the (two-sided) risk of any deviation in total return relative to expected total return. In the default loss insurance case, the financial institution is insuring specifically against the (one-sided) risk of default loss in excess of expected default loss. We will show below that in general the premiums for unexpected total return risk transfer and unexpected default loss insurance are different.

Properties of Credit Risk Premiums

To further motivate the concept of credit risk premiums, we summarize their primary properties in what follows. To begin with, if the cash flows associated with a credit instrument are deterministic, then the associated risk premium should be zero. We see that this condition holds for our definition, since, if cash flows are riskless, the natural measure and risk-neutral measure are equivalent (i.e., have the same sets of measure zero). If only one particular outcome is possible under a given measure, then only that same outcome is possible under an equivalent measure. Consequently, if there is no risk, there can be no risk premium.

We observe that risk premiums can be negative. Consider the situation in which a lender holding a high risk loan enters into a credit default swap to hedge his credit risk. The loan has a positive risk premium because the loan creates a credit risk exposure. The credit default swap (as viewed by the lender) has a negative risk premium because it offsets credit risk. Of course, from the standpoint of the credit default swap counterparty who now holds the default risk, the deal has a positive risk premium.

One may reasonably postulate that the loan risk premium and the credit default swap risk premium exactly offset each other. As the numerical examples below demonstrate, this won’t generally be the case. The net position (loan + credit default swap) isn’t always perfectly hedged. The loan spread and the swap spread may differ. In that case, the lender acquires protection against default loss, but not against the "basis" risk inherent in the spread differential.

Net present value is additive in the restrictive sense that the NPV of two pooled cash flows tied to the same borrower rating migration process is the sum of the NPV’s of the component cash flows. Furthermore, expectation is a linear operator. Consequently, one can calculate the risk premium for a hedged position relative to a single credit exposure as the sum of the risk premiums of the separate instruments comprising the hedge.

We next show that risk premiums as we have defined them generalize the notion of marginal risk premiums. Consider a one-year term loan and let
 

In the present context, we treat LIED as deterministic. We also assume that any interest payment due at the time of default is paid in full.

We now define the marginal risk premium  associated with a loan originated to a borrower with risk grade i as

.            (2)

Thus,  represents the excess of the par credit spread over the expected default loss, where we have calculated expected default loss with respect to the natural migration measure. The term "marginal" here indicates that  represents the incremental risk premium the lender earns per $1 of loan principal if the term of the loan is extended by one year.

Under the risk-neutral measure, the one-year default probability  becomes (see [3]).

           (3)

It then follows that
 
 

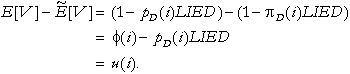           (4)

For the same one-year loan, the UDL risk premium is given by
 

              (5)

A comparison of (4) and (5) shows that the UDL risk premium and UTR risk premium differ by . Since the par credit spread  is necessarily less than LIED, this difference is a positive quantity. We shall see below, however, that it is not the case for multi-period loans that the UDL risk premium is always larger than the UTR risk premium.

To investigate the properties of risk premiums for multi-period loans, we have constructed a spreadsheet that calculates the expected present values for the cash flows of a simple (option-free) two-year term loan. We assume a rating system with eight possible risk grades: Aaa, Aa, A, Baa, Ba, B, Caa, and default, and assume the average (1920-1996) one-year migration matrix (conditional upon no rating with-drawal) given in [6]. To focus on risk, we ignore costs of loan origination or costs of carry (servicing and monitoring). Our results reflect the case  and  per annum.

The assumed marginal risk premiums (taken to have a flat term structure) and the resulting par credit spreads are shown in the following table:

Risk Rating at Loan Origination
 

	Aaa	Aa	A	Baa	Ba	B	Caa
One-Year Expected Default Loss	0.4 bps	2.8	5.6	12.4	50.0	154.8	552.4
Marginal Risk Premiums	0.1 bps	0.3	1.1	2.2	10.0	45.0	110.0
One-Year Par Credit Spreads	0.5 bps	3.1	6.7	14.6	60.0	199.8	662.4
Two-Year Par Credit Spreads	0.7 bps	3.3	7.2	16.4	63.9	202.8	642.4

 

The one-year par credit spreads are obtained for each rating grade by summing the expected loss component and the unexpected loss (marginal risk premium) component. Observe the term effect that the two-year par credit spreads are higher than the one-year par credit spreads for every initial rating grade but Caa. The reason is that if a Caa credit does not default in year one, there is a .092 conditional probability of a year 1 upward migration (based on the one-year migration matrix in [6]), and a corresponding reduction in the second-year exposure relative to the first-year exposure. For all other rating grades, the risk of a downward migration in year 1 dominates that of an upward migration and the second year exposure is higher than the first.

We first compare the UTR risk premium and UDL risk premium as a function of initial rating grade for the two-year loan with an assumed principal of $10,000. The results are shown in Table 3.

Unexpected Default Loss Risk Premium

Risk Rating at Loan Origination
 

	Aaa	Aa	A	Baa	Ba	B	Caa
UTR Risk Premium	$.23	$.66	$2.21	$4.79	$20.46	$82.62	$187.85
UDL Risk Premium	$.23	$.66	$2.21	$4.78	$20.32	$80.54	$171.75

As one would expect, the loan risk premiums are quite small for low risk borrowers, but increase significantly as the credit quality of the borrower deteriorates. At an Aaa borrower risk rating, the UTR risk premium and UDL risk premium are each about 0.2 bps relative to the $10,000 loan principal. At a Caa rating, both risk premiums increase dramatically to more than 170 bps.

One observes that transferring unexpected total risk for a two-year loan commands a premium at least as large as that required to insure only unexpected default loss risk. This contrasts with the case of a one-year loan, where we showed earlier that the opposite relationship holds. The explanation lies in the fact that the only risk in a one-period loan is default loss risk (the first year interest is assumed to be effectively prepaid). If the financial institution buys unexpected default loss insurance, it keeps the unexpected gain when default does not occur. If the financial institition enters into an unexpected total return swap, it must pay that unexpected gain to the counterparty at settlement. As a result, the UTR risk premium is higher on the one-period loan than the UDL risk premium.

In the case of a two-year loan, both the return of principal and the second year interest payment are at risk. A UTR swap protects against both risks. UDL insurance protects only against the loss of loan principal. The results indicate that the protection which the UTR swap provides against loss of interest in year 2 and which is absent from the UDL policy more than offsets the settlement cost if the loan matures without default. The risk premium differential is barely discernible at the higher rating grades, but becomes increasingly significant as one progresses down the rating scale.

We next examine the effect of loan pricing on the loan risk premium. (In what follows, all references to risk premiums will be to UTR risk premiums.) We assume a loan with principal $10,000 to a Caa borrower and determine the risk premium for  basis point variations in the loan spread relative to par. The results follow.
 

Loan principal: $10,000

Borrower risk rating: Caa

Loan Spread (bps)	Risk Premium
	$185.34 $513.76
	$187.85 $$
	$190.36

In the case of a Caa borrower, the effect of spread on risk premium is about 2.5 bps of risk premium per 100 bps of spread variation. The effect of spread on risk premium rapidly diminishes with increasing risk grade and all but vanishes at the investment grade end of the risk spectrum.

We next explore the effect of hedging on risk premiums. We consider three alternative lender strategies: (i) hold only the loan and bear the full credit risk, (ii) enter into a credit default swap (at par) to hedge the credit risk on the loan, or (iii) purchase a default put to hedge the loan risk. In the case of the credit default swap, the holder of the loan pays a fixed spread to the counterparty to insure against credit loss. The spread is paid annually until the loan either matures or defaults (the possibility of prepayment of the loan by the borrower has been ruled out). In the current context, we use the term "put" to refer to the case in which the holder of the loan makes a single upfront payment to the counterparty to purchase credit loss insurance for the term of the loan.

In Table 5 we show the risk premium for each of these three exposures and for each borrower risk rating at loan origination. Both the loan and the credit default are assumed to be priced at their par spreads under risk-neutral pricing. The default put is priced at its risk-neutral market value. Again the loan principal at origination is taken to be $10,000.

The hedge position consisting of the loan + default has a zero risk premium independent of the borrower rating. This is what one would expect, because the par spread on the loan and the par spread on the credit default swap are equal. The spread the lender earns from the borrower exactly offsets the payments he makes to the swap counterparty. In addition, any loss of principal resulting from borrower default is offset by a payment from the swap counterparty. The net effect is that the lender simply earns the risk-free rate in all cases.
 

Risk Rating at Loan Origination
 

	Aaa	Aa	A	Baa	Ba	B	Caa
Loan	$.23	$.66	$2.21	$4.79	$20.46	$82.62	$187.85
Loan + Default Swap Swap	0	0	0	0	0	0	0
Loan + Default Put	<$.01	<$.01	<$.01	$.01	$.14	$2.08	$16.10

 

The loan + default put is an incomplete hedge, since the cash flows have some residual degree of risk. If the borrower defaults, the lender is protected against any loss of principal. However, if the loan defaults in year one, the lender loses the interest that would have been paid in year 2. As Table 5 indicates, this risk of loss of loan income is very much a function of the borrower risk rating.

A comparison of Tables 3 and 5 shows that the (UTR) risk premium for the loan + default put hedge is equal to the excess of the UTR risk premium on the loan over the UDL risk premium on the loan. This follows from a combination of (i) the fact that the UDL risk premium on the loan is the same as the UTR risk premium on the default put and (ii) the applicability of risk premium additivity.

In summary, the point of view we have taken is that the credit risk associated with a credit instrument can be measured by the cost for the holder to enter into a form of swap which transfers to the counterparty the risk of any variation (positive or negative) between the actual return that instrument generates and its expected return. Credit risk can be "self-insured," in which case the "counterparty" is the holder’s risk capital, or swapped to a true counterparty through a form of credit derivative. In either case, the risk premium is what the holder must pay at arbitrage-free market pricing to effect the complete transfer of the credit risk.

In Part II of this article we will develop in greater detail the relationship between credit risk premiums and portfolio value at risk. We will show how that relationship leads to a method for estimating risk-adjusted returns at the transaction level and provides a natural link between transaction credit risk and portfolio value-at-risk.

References